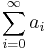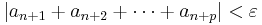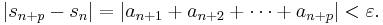Cauchy's convergence test

The Cauchy convergence test is a method used to test infinite series for convergence. A series

$\sum_{i=0}^\infty a_i$

with real or complex summands a_i is convergent if and only if for every 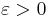$\varepsilon>0$ there is a natural number N such that

$|a_{n%2B1}%2Ba_{n%2B2}%2B\cdots%2Ba_{n%2Bp}|<\varepsilon$

holds for all n > N and p ≥ 1.

The test works because the space R of real numbers and the space C of complex numbers (with the metric given by the absolute value) are both complete, so that the series is convergent if and only if the partial sum

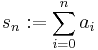
$s_n:=\sum_{i=0}^n a_i$

is a Cauchy sequence: for every 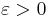$\varepsilon>0$ there is a number N, such that for all n, m > N holds

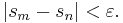
$|s_m-s_n|<\varepsilon.$

We can assume m > n and thus set p = m - n. The series is convergent if and only if

$|s_{n%2Bp}-s_n|=|a_{n%2B1}%2Ba_{n%2B2}%2B\cdots%2Ba_{n%2Bp}|<\varepsilon.$

This article incorporates material from Cauchy criterion for convergence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.